Geodesics on \({SL}(n)\) with the Hilbert-Schmidt metric, and one application to fluids

Geodesics on \({SL}(n)\) with the Hilbert-Schmidt metric, and one application to fluids

Willie Wai Yeung Wong
wongwwy@math.msu.edu
Michigan State University

Slides available :   https://slides-n-notes.qnlw.info

Credits page

• Joint work with:
  • Audrey Rosevear, Amherst College
  • Samuel Sottile, Michigan State University
• Support by NSF through the SURIEM (2020) summer REU site at MSU.
• Paper to appear in La Matematica; arXiv:2101.09266.

Audrey will present a poster on this at JMM2022; do stop by and say hi!

Outline

1. Set-up
2. Physics
3. Geometry; prior results
4. Our results
5. Application; what's next?

1. Set-up

Dramatis personae

• $M(n)$ — space of $n\times n$ real matrices
• $S(n)$ — symmetric elements of $M(n)$
• $SL(n)$ — determinant 1 elements of $M(n)$
• $SO(n)$ — elements of $SL(n)$ satisfying $A^T = A^{-1}$
• $\mathring{S}_+(n)$ — positive definite elements of $S(n) \cap SL(n)$
• $\mathfrak{sl}(n)$ — trace 0 elements of $M(n)$
• $\mathfrak{so}(n)$ — anti-symmetric elements of $M(n)$
• $\langle A, B\rangle := \mathrm{tr}(AB^T)$ — Hilbert-Schmidt inner product on $M(n)$

Hilbert-Schmidt metric on $SL(n)$

$M(n)$ with $\langle A,B\rangle$ $\qquad\cong\qquad$ $\mathbb{R}^{n\times n}$ with standard metric.

$SL(n)$ is a co-dimension 1;
induced Riemannian metric — the HS metric.

Not bi-invariant!
(Non-compact, but semi-simple, so Killing form is pseudo-Riemannian.)

The Question

What is the geometry of this Riemannian manifold?

1. Geodesic completeness? — ✓
2. Existence / stability of bounded geodesics?
3. Asymptotic behavior and stability of unbounded geodesics?

Why emphasis on geodesics?

2. Physics

Rigid Body

Rigid Body

• Initial/reference body: \(\quad \Omega\Subset\mathbb{R}^n\)
  Center of mass condition: \(\displaystyle \quad \int_\Omega y ~\mathrm{d}y = 0\)
• Configuration at time \(t\): $\quad x(t) + A(t)\cdot\Omega; \qquad x(t)\in \mathbb{R}^n, \quad A\in SO(n)$
• Total kinetic energy: \[ \int_{\Omega} |x'(t) + A'(t)y|^2 ~\mathrm{d}y = \mathrm{vol}(\Omega) |x'(t)|^2 + \mathrm{tr}\left( A'(t) I_\Omega A'(t)^T \right)\]
• Moment of inertia: \(\quad \displaystyle I_\Omega = \int_\Omega y y^T ~ \mathrm{d}y\)

For write-up with more details: click here.

Action Principle

\[ S = \int \left[ \mathrm{vol}(\Omega) |x'(t)|^2 + \mathrm{tr}\left( A'(t) I_\Omega A'(t)^T \right) \right] ~dt\]

The integrand defines a positive definite quadratic form on the tangent space of $\mathbb{R}^n\times SO(n)$

Solutions are geodesics w.r.t. this Riemannian metric.
Note that the metric given by $I_\Omega$ is not the bi-invariant metric on $SO(n)$.

Motion on $\mathbb{R}^n$ decouples from motion on $SO(n)$.

Affine Motion

• Allow the body to also deform linearly but preserving volume.
• Swap $SO(n)$ with $SL(n)$.
• Everything else the same: $I_\Omega$ induces a Riemannian metric on $SL(n)$ which determines the trajectories.

Why do we only care when $I_\Omega = \mathrm{Id}_n$?

Incompressible Fluids

• Allow the body to arbitrarily deform, but preserving infinitesimal volume.
• Replace $SO(n)$ by the group(oid) of volume preserving diffeomorphisms.
• For fluid flow inside a fixed domain $\Omega$: Euler-Arnol'd equations.
• Free boundary problem: requires boundary conditions.
  • At any fixed time: fluid pressure is constant along (moving) boundary.

Relating affine motion to fluid motion

• $SL(n)$ is a subgroup of the group of volume preserving diffeos of $\mathbb{R}^n$.
• Boundary conditions satisfied by $SL(n)$ geodesic $\iff$ under the Riemannian metric induced by the geometry of $\Omega$, $SL(n)$ is totally geodesic.
• Theorem. This holds iff $\Omega$ is a round ball (and hence $I_\Omega = \mathrm{Id}_n$).

3. Geometry; prior results

Discrete symmetry

\(A \to A^T\) is isometry of \(M(n)\), and fixes \(SL(n)\), so is isometry on \(SL(n)\).

Lemma. $S(n)\cap SL(n)$ is totally geodesic in \(SL(n)\).

Corollary. $\mathring{S}_+(n)$ is totally geodesic in \(SL(n)\).

Continuous symmetries

• \(SO(n)\) acting on \(M(n)\) by matrix multiplication is isometric & fixes \(SL(n)\)
• Distinct left and right actions!
  • Generate a total of \(n(n-1)\) Killing vector fields
  • Physical interpretation: $\quad$ angular momentum and vorticity
• Conjugate action: $A \mapsto OAO^{-1}$ (fixes $\mathring{S}_+(n)$)
• Composite action: $A \mapsto OAO$ (not faithful)

Polar decomposition

Every $A\in SL(n)$ has a unique factorization as $OP$ (or $PO$): $ \begin{cases} O\in SO(n) \newline P\in \mathring{S}_+(n)\end{cases}$

$SL(n)$ foliated by cosets

So the geodesics are easy to describe, right?

Problem: Left actions generate right-invariant vector fields and vice versa

... so even with our conserved quantities, the motions on the two factors do not split.

$n = 2$ is special: analysis

• Motion is completely integrable: $\dim(SL(2)) = 3$ and conservation of
  • Energy
  • Angular momentum
  • Vorticity
• Used in Roberts-Shkoller-Sideris (CMP 2020) where geodesics are fully classified.

Will return to this classification a bit later.

$n = 2$ is special: geometry

• $SL(2)$ is a warped product $\mathring{S}_+(2) \times_f \mathbb{S}^1$
• Use the composite $A\mapsto OAO$ action
  • double cover of $SL(2)$ by $\mathring{S}_+(2) \times_f SO(2)$.
  • Use $SO(2) = U(1)$ and "take square roots"
• $SO(2)$ is abelian:
  • Composite $OAO$ action is orthogonal to cosets of polar decomposition
  • Conjugate $OAO^{-1}$ action is tangent to cosets
• Decompose as integrable motion on $\mathring{S}_+(2)$ plus fibre motion.
• (Private communication from Ben Schmidt)

Definitions

Throat

Call $SO(n)\subsetneq SL(n)$ the "throat": it describes the points closest to the origin in $M(n)$.

Second fundamental form

Sign convention: $II(X,X) \gt 0$ if it curves away from the origin.

Second f.f. defined via normal pointing away from origin of \(M(n)\).

Geodesic equation

Let $X,Y\in T_A SL(n)$, then \[ II(X,Y) = \frac{\mathrm{tr}(A^{-1}X A^{-1}Y)}{|A^{-1}|} \] and the geodesic equation reads \[ \ddot{A} = \frac{ \mathrm{tr}( A^{-1} \dot{A} A^{-1} \dot{A})}{\mathrm{tr}(A^{-1} A^{-T})} A^{-T}.\]

$n = 2$ geodesic classification

• The only bounded geodesic orbits the throat
• There exists semi-bounded geodesics converging to the throat
• All unbounded geodesics are "asymptotically linear" ($II(\dot{\gamma},\dot{\gamma}) \to 0$)

How much of these survive in higher dimensions?

$n = 3$ prior results

Analyses of some special explicit solutions and their asymptotics

Sideris (ARMA 2017)

$n$-independent prior results

• Virial Identity: let $A: t\to M(n)$ a $SL(n)$-geodesic \[ \frac{d^2}{dt^2} |A|^2 = \frac{|\dot{A}|^2}{|A|} + \frac{n}{|A|^2} II(\dot{A}, \dot{A}).\]
• Proposition: if additionally $A$ is such that $II(\dot{A}, \dot{A}) \gt 0$ for all $t \gt t_0$, then $A$ is unbounded and asymptotically linear.

Sideris (ARMA 2017)

4. Our results

Higher dimensions are more curvy

• Theorem. $SL(2)$ has bounded sectional curvature.
• Theorem. When $n \geq 3$, given $A\in SL(n)$ and $W\subset T_A SL(n)$ a plane, denote by $k(W)$ its sectional curvature. Then:
  1. $k(W) \leq |A^{-1}|^2$ for all $(A,W)$;
  2. There exists a sequence $(A_i, W_i)$ with
     $|A_i^{-1}| \to \infty$ and $\liminf k(W_i) |A_i^{-1}|^{-2} \geq \frac14$.
  (Remark: the function $A\mapsto |A^{-1}|$ is proper.)

Linear solutions are linearly stable

• Linear solutions: those whose images are lines in $M(n)$.
  All in the form on $A(t) = A_0(\mathrm{Id} + t M)$ where $M$ nilpotent.
• Linear stability: Jacobi fields along such curves grow at most linearly.
• Key step: showing for such $A(t)$ the quantity \[ \left| \mathrm{Riem}(\dot{A}, J, \dot{A}, K) \right| \lesssim \frac{|J|~ |K|}{(1 + t^4)}. \]

Bounded geodesics abound in $n \geq 4$

• Theorem. When $n = 2m \geq 4$, for every $\eta \geq |\mathrm{Id}|$, there exists a bounded geodesic $A(t)$ with $|A(t)| \equiv \eta$.
• In fact, we can write $A(t) = A_0 \exp (Ct)$ with $A_0 \in \mathring{S}_+(n)$ and $C\in \mathfrak{so}(n)$.
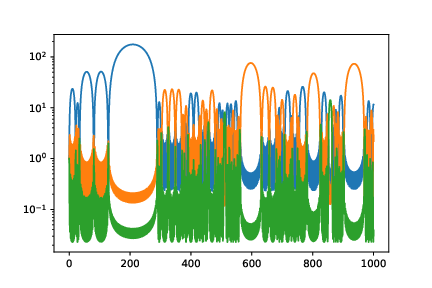
• Remark: these are the only "non-linear" "exponential" solutions.
• Physical picture: Stationary fluid solution; an ellipsoid with "paired" axes, spinning separately in each plane.
• When the rotational speeds are not "tuned", the solutions remain bounded, but pulsates.

Refinement of Virial argument

\[ \frac{d^2}{dt^2} |A|^2 = \frac{|\dot{A}|^2}{|A|} + \frac{n}{|A|^2} II(\dot{A}, \dot{A}).\]

Lemma. When $n = 2$, we have $\frac{d^2}{dt^2} |A(t)|^2 \leq 0 \implies |A(t)| = |\mathrm{Id}|$.

Corollary. All geodesics except for the throat rotation are unbounded.

Emphatically false when $n \geq 3$.

Virial revisited

Theorem. [sufficient conditions for unboundedness]

1. Solution is tangent to $\mathring{S}_+(n)$ (or another coset)
2. Solution has vanishing total angular momentum
3. Solution has vanishing total vorticity

New formulation of equations

Given solution $A(t)$, define \[ \beta = A^{-1}A^{-T}, \quad \omega = A^T \dot{A} + \dot{A}^T A, \quad \zeta = A^T \dot{A} - \dot{A}^T A \]

• $\beta$: "square" of the "radial component" in polar decomposition
• $\omega$: "radial" velocity
• $\zeta$: "angular" velocity

Above is the vorticity version; angular momentum version moves the transpose to the other factor.

Cannot do both simultaneously.

New formulation of equations

Solves problem with Killing vector field not pointing in the fibre direction.

\begin{align*} \frac{d}{dt} \beta & = -\beta \omega \beta \newline \frac{d}{dt}\omega & = \frac12(\omega + \zeta)^T\beta(\omega + \zeta) + \underbrace{\frac{\mathrm{tr}\omega\beta\omega\beta}{2\mathrm{tr}\beta}}_{\geq 0} I + \underbrace{\frac{\mathrm{tr}\zeta\beta\zeta\beta}{2\mathrm{tr}\beta}}_{\leq 0} I \newline \frac{d}{dt}\zeta &= 0 \end{align*}

Compatibility condition: $\quad \mathrm{tr}\beta\omega = 0$.

Preserves "block diagonal structure"

Block diagonal solutions

Assume $\beta, \omega,\zeta$ decompose into $2\times 2$ blocks (with one $1\times 1$ block when $n$ is odd) along the diagonal.

A boundedness criterion

Theorem. Let $n$ be even. If the initial data of $\beta,\omega$ are built from $2\times 2$ blocks that are pure-trace, and if $\zeta$ has no vanishing bocks, then the solution is bounded.

When $n = 2$, hypothesis only possible with rotation at throat.

"Swirling and shear flows"

Theorem. If the initial data has the form \[ \beta_0 = \begin{pmatrix} b_1 \mathrm{Id}_{2m} \newline & b_2 \mathrm{Id}_{n - 2m}\end{pmatrix}, \quad \omega_0 = \begin{pmatrix} w_1 \mathrm{Id}_{2m} \newline & w_2 \mathrm{Id}_{n-2m} \end{pmatrix} \] and writing $\varepsilon$ for the antisymmetric $2\times 2$ matrix \[ \zeta_0 = \begin{pmatrix} z (\underbrace{\varepsilon \oplus \cdots \oplus \varepsilon}_{m \text{ copies}}) \newline & 0 \end{pmatrix};\] then the corresponding solution is unbounded, and asymptotically linear.

Sideris [ARMA 2017] described $n = 3$ and $m = 1$ with explicit integration

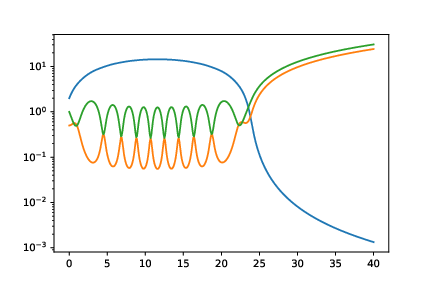
Further generalization?

5. Application; what's next?

Asymptotically linear solutions can be unstable

• Let $A(t)$ be a swirling and shear flow: we can show that $II(\dot{A}, \dot{A})$ is eventually positive.
• So $A(t)$ is "asymptotically linear"
• "Small perturbations" \[ \zeta_0 = \begin{pmatrix} z (\underbrace{\varepsilon \oplus \cdots \oplus \varepsilon}_{m \text{ copies}}) \newline & 0 \end{pmatrix} \Longrightarrow \begin{pmatrix} z (\underbrace{\varepsilon \oplus \cdots \oplus \varepsilon}_{m \text{ copies}}) \newline & \delta (\varepsilon \oplus \cdots \oplus \varepsilon) \end{pmatrix} \]
• Non-vanishing rotation $\implies$ motion is bounded

Connection to fluids

• Bounded motions must enter regime with negative second fundamental form.
• Physical instability: Rayleigh-Taylor. (Require pressure just inside the boundary be positive.)

Further questions

• Conjecture. When $n$ is odd, $SL(n)$ has no bounded geodesics.
• Conjecture. The only solutions with $|A(t)|$ constant are those we found.
• Question. Do there exist unbounded geodesics which are not asymptotically linear when $n \gt 2$?
• Question. Do there exist "heteroclinic orbits"?

Thank you!